In performance marketing, attribution refers to repartition of revenue to marketing channels, for return-on-investment (ROI) calculations.
While most attribution schemes are rule-based, we here present a data-driven scheme.
Context
The attribution problem was first presented in our previous article: Using alternative attribution models
To sum it up, with increasingly numerous digital marketing channels (about 40 for Sephora Digital !), deriving ROI for each of them is a real hassle.
In other terms, if a customer
- opens an e-mail from a campaign
- clicks on a Facebook advertisement
- enters the sephora.sg through Google Adwords
- then ends up spending $100
$\rightarrow$ How would you credit this revenue to the different touchpoints ?
Being able to attribute revenue to marketing channels accurately allows for performance review of marketing channels. It can be used as a guide for budget effort repartition.
Most popular schemes for attribution are rule-based, and perfomed at the level of the order. Here are some examples :
- First-click : e-mail campaigns would be credited with $100 return
- Last-click : Adwords would be credited with $100 return
- Uniform : e-mail campaigns, Facebook ads, Adwords would be credited with $33
- 40-20-40 (aka. U-shape) : e-mail campaigns and Adwords would be credited with 40% each, Facebook ads with 20%
Many more rule-based scheme could be made up. These rely mostly on common sense and market knowledge.
Even though there is no objective way of accessing the accuracy of an attribution model, other data-driven attribution heuristics have been proposed.
Today, we present how Markov Chains can be used to derive an attribution model.
Markov Chains
Presentation
Markov Chains (MCs) are statistical models for sequences of finite states. Here, we will only deal with the most common type of MCs, which are first-order MCs :
Given a finite set $S$ of $n$ states
a sequence of $m$ states
A MC modelisation of such a sequence is
where
$p((\sigma_i)_{1\le i\le m})$refers to the probability of occurence of sequence$(\sigma_i)_{1\le i\le m}$$p(\sigma_{i+1}|\sigma_{i})$refers to transition probability from state$\sigma_{i}$ to $\sigma_{i+1}$
As you see, transition probabilities define a MC model and reflect the core concepts of MCs:
“Probability of hopping from state $\sigma_i$ to $\sigma_{i+1}$ only depends on $\sigma_i$, not on the previous states, hence the name first-order MCs."
Transition matrix
For a MC, transition probabilities can be combined into a transition matrix $T$:
A nice property of transition matrices is
where $p_p(s_l|s_k)$ is the probability of hopping from $s_k$ to $s_l$ in $p$ steps (exactly).
“But how does it relate to the attribution problem ?"
Application to customer journey modeling
Adaptation to context
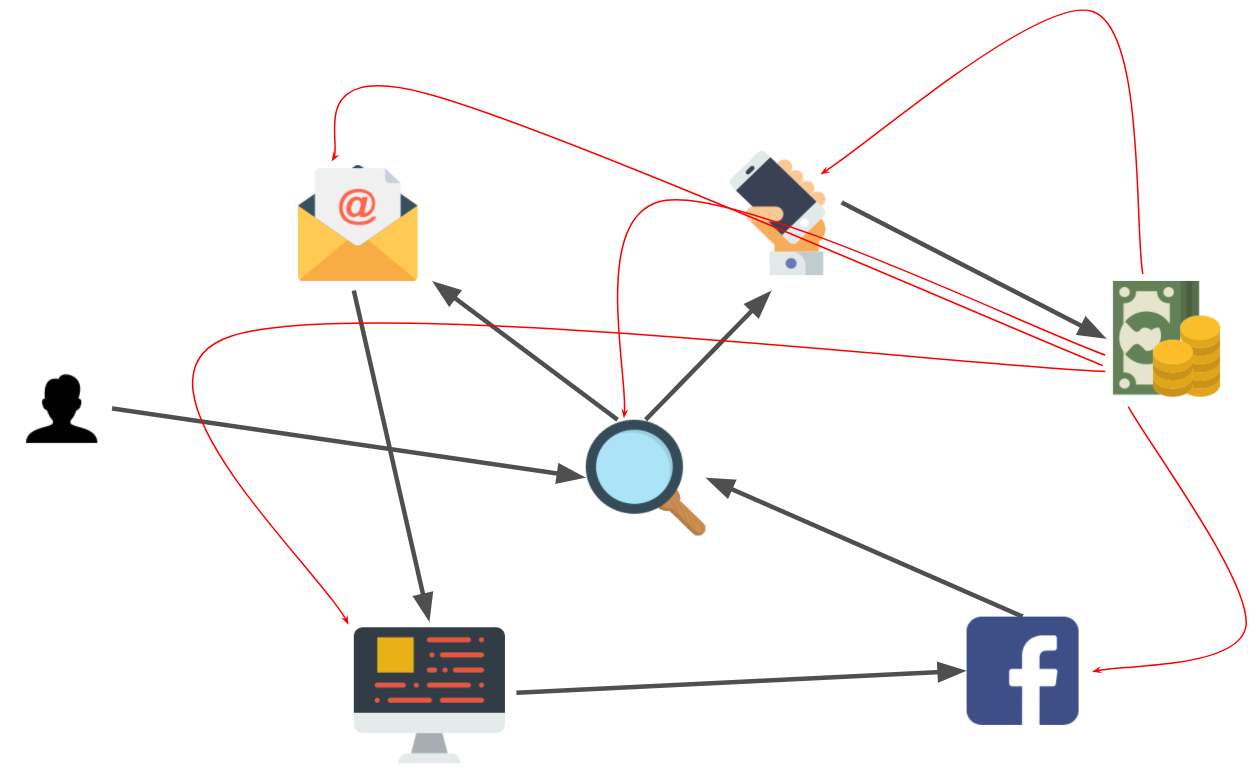
A customer journey can be modeled as a succession of marketing touchpoints.
We consider the following touchpoints :

An example of customer journey :

Each touchpoint can be seen as a state, and a customer journey as a MC sequence of states, hence the modelisation of the probability of such a journey :

” A customer journey can be actually seen as a MC realization ! “
Remember that a MC is defined by its states and transition matrix.
MCs can be adapted to customer journeys, with the states:
- starting state
- channels
- (non-)conversion states
This transition matrix is learnable from our past customer journey data.
The output can represented as a network of states and weighted directed edges.
Here is a (simplified) visualization:
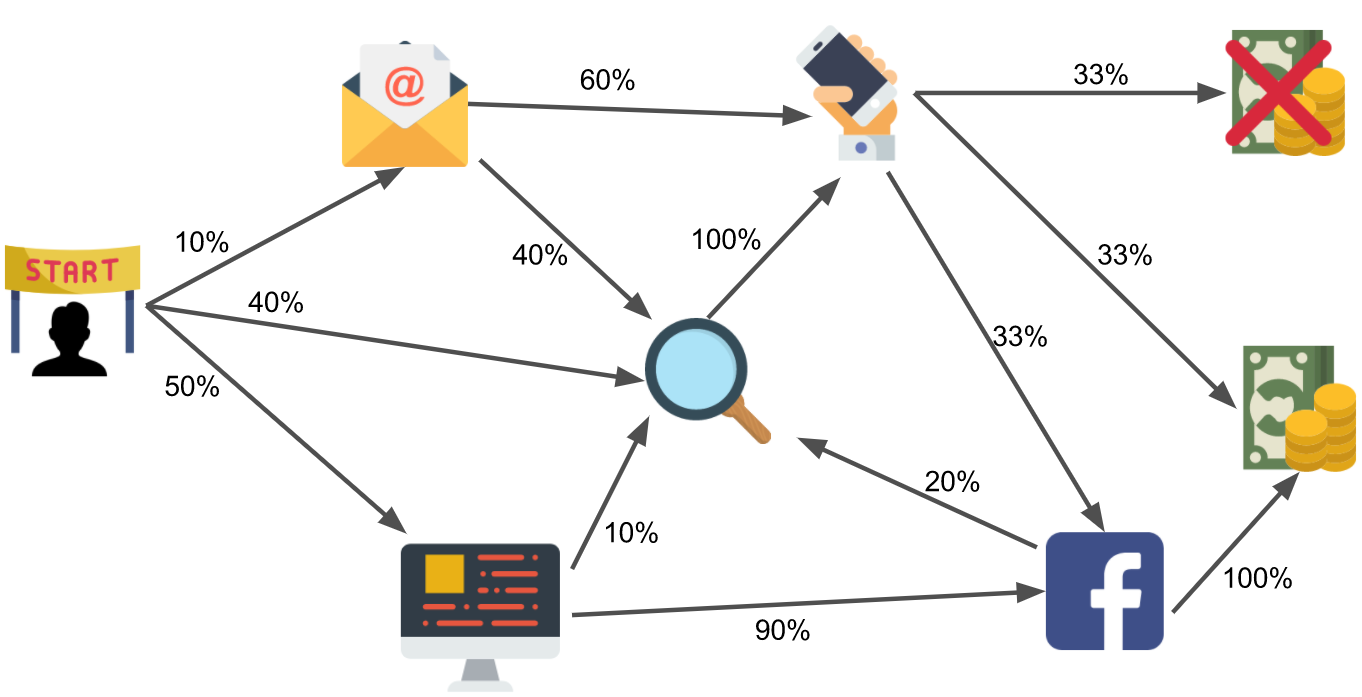
From this network, random walks, representative of historical customer journeys, can be generated. Some of them will end up converting, some not.
” I still do not see the link with attribution models… “
MCs and attribution
Imagine removing the Google Adwords channel from the network.
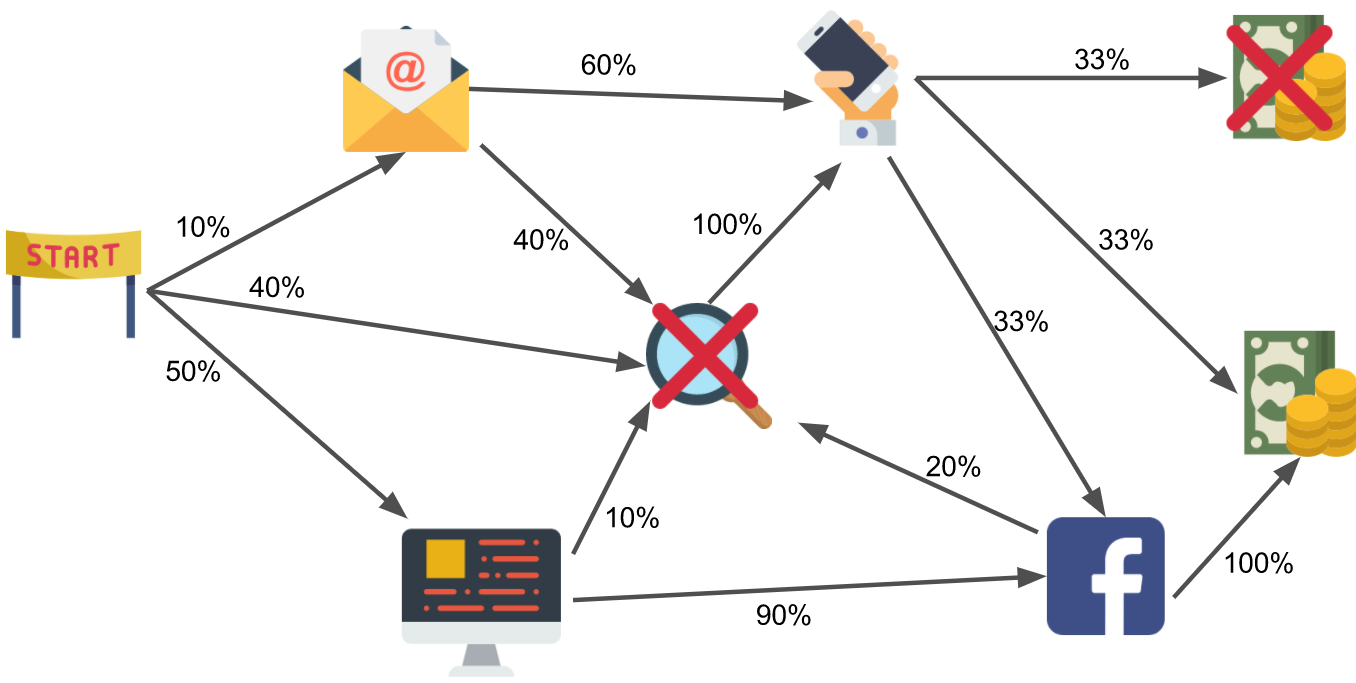
$\rightarrow$ By considering random walks that encounter state Google Adwords as non-converting, random walks are less likely to convert.
We define the removal effect of a channel as
where
$rate_{init}$is the original conversion rate$rate_{removal}$is the conversion rate after channel removal
Therefore, the stronger the removal effect, the stronger the attribution.
After re-normalizing removal effects of each of the channels to one, total revenue can then be distributed among channels.
To go further
Some key points for making it work are lacking here, like:
- Learning the transition matrix
- Compute likelihood of conversion given a MC model, with and without removal
If these are points of interest, the Data Team is here to help :)
– Sylvain